Convolutional Neural Networks - 1 week
Computer Vision
컴퓨터 비전은 딥러닝의 분야 중 하나로 시각적인 분야를 컴퓨터에 학습시키는 분야다
얼굴 인식, 신원 확인, 자율 주행 자동차 등등..
지금까지 했던 고양이 분류, 자동차 분류도 모두 여기에 해당한다
Edge Detection Example
Convolutional operation을 edge detection을 하며 알아보자
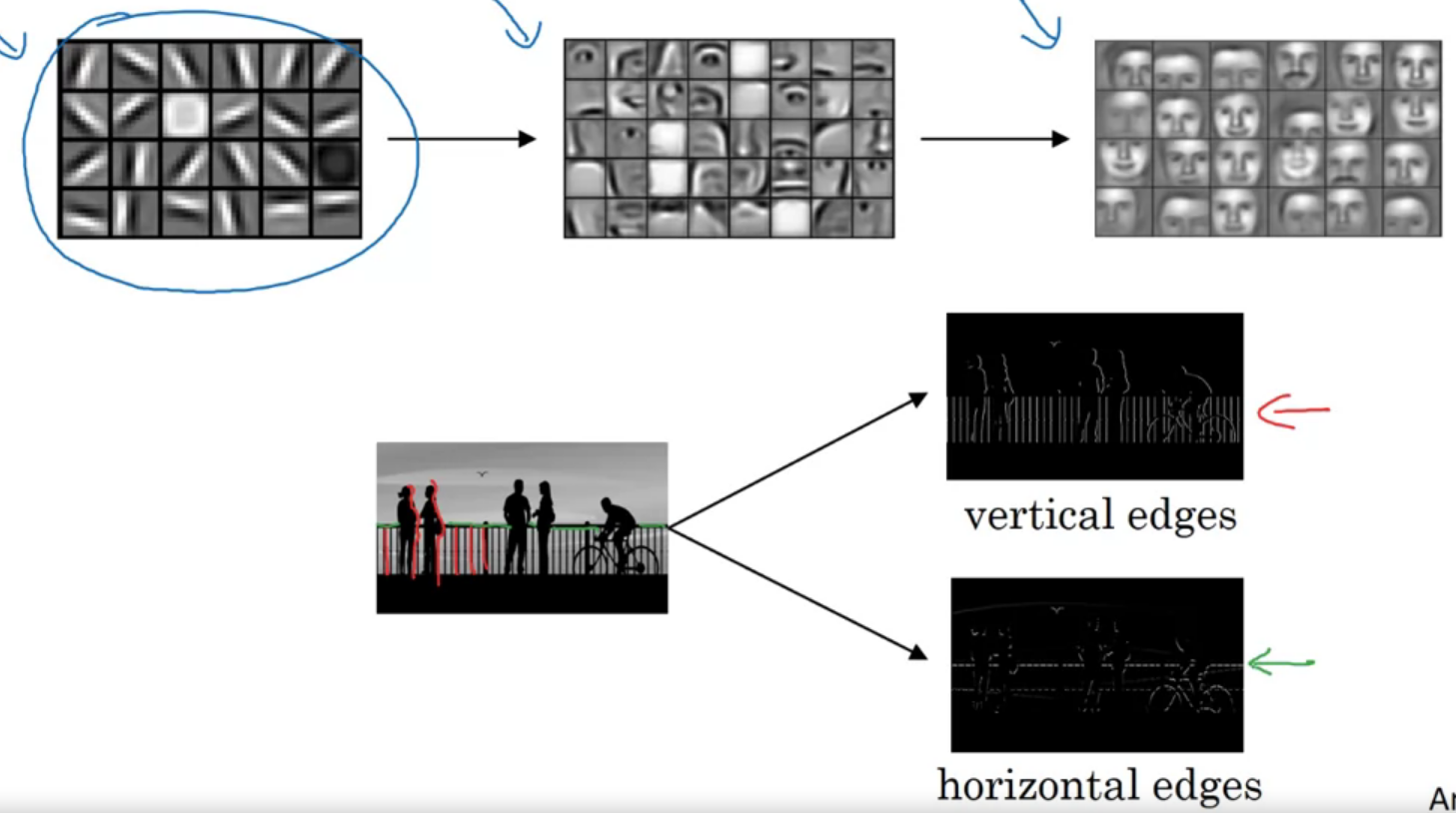
이미지에서 어떻게 저렇게 수직, 수평 테두리를 검출해 낼 수 있을까
필터나 커널을 이미지에 convolution을 통해 얻을 수 있다
수직선 검사 예시를 보자

결과 행렬은 필터를 이미지에 원소곱 해서 얻는다
뭘 한지 모르겠으니 간단한 숫자로 알아보자

합성곱을 시행하자 가운데 색이 바뀌는 부분의 수치가 크게 나타난다
More Edge Detection
positive edge와 negative edge의 차이를 배우고, 구현해보자
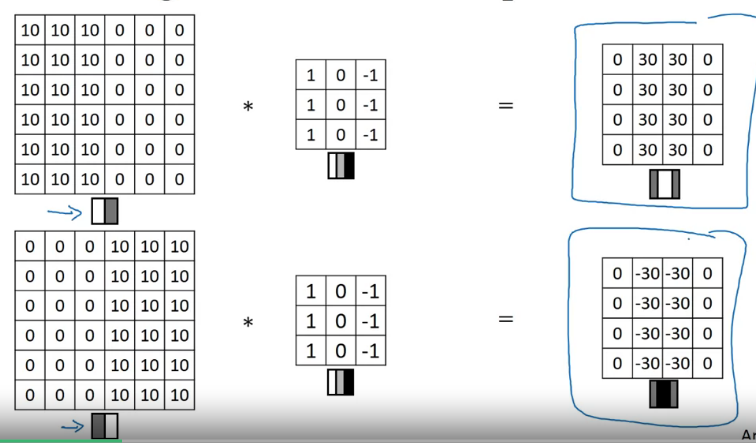
밝은 곳에서 어두운 곳으로 가면 positive edge, 반대의 경우 negative edge라고 하나보다(아마도...)
수평과 수직 edge 검사엔 아래와 같은 사용 한다


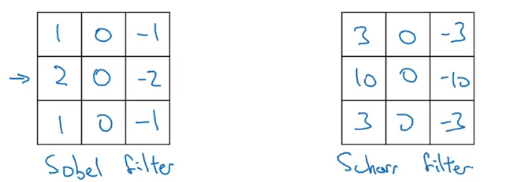
물론 필터에 가중치를 주어 학습할 수 있다
Padding
\((n\times n\)) 이미지를 \((f\times f)\) 크기의 필터로 convolving 하면 \(((n-f+1)\times (n-f+1)\))크기의 결과 행렬이 출력될 것이다
이 과정에는 합성곱 연산을 할 때마다 크기가 축소되고, 가장자리 픽셀 정보가 버려지는 문제가 있다
위아래로 픽셀을 추가하여 이를 해결할 수 있다
이를 패딩이라고 한다 (p = padding amount)
패딩이 없다면 valid convolution, 패딩하여 크기를 유지시켜주면 same convolution(\(p={f-1\over 2}\))이라 한다
필터 크기는 대부분 홀수라고 한다 (비대칭 패딩을 해야 하고, 중심을 가지는 게 좋기 때문이라고 한다)
Strided Convolutions
stride는 필터를 계산하며 건너뛰는 칸의 수이다 (위에선 1이었다)
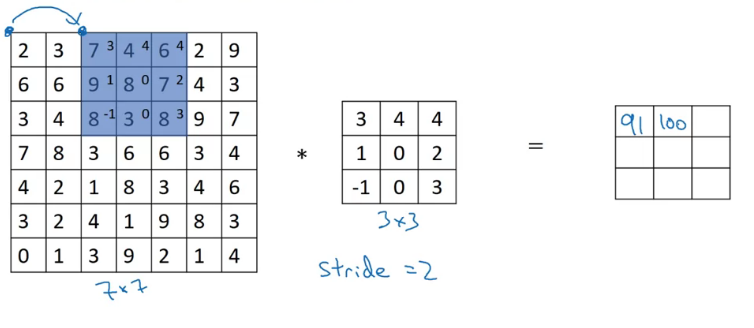
\((n\times n)\) 이미지를 \((f\times f)\) 필터로, p 패딩과 s 스트라이드로 합성곱을 시행하면 \(({n+2p-f\over s}+1 \times{n+2p-f\over s}+1)\)
정수가 아니라면 내림해준다, 즉 마지막에 칸이 모자라면 건너뛴다
Convolutions Over Volume
3차원 행렬 이미지 (RGB도 있음!) 합성곱을 배워보자
이미지의 차원이 변했으니, 특징을 찾기 위해선 필터도 차원이 추가되어야 한다
(height x width x # channels)으로 차원을 부를 것이다
이미지와 필터의 channel 수는 동일해야 한다
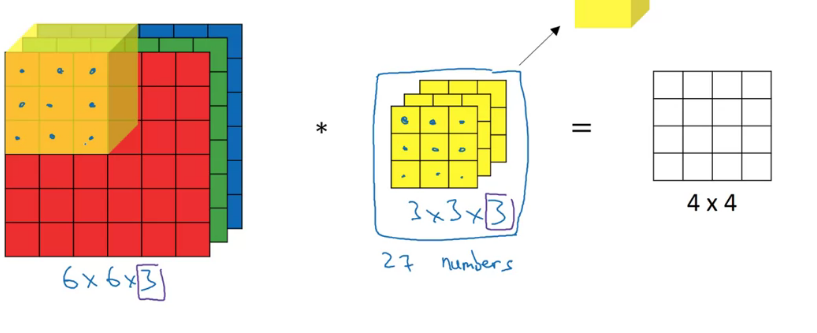
하나의 색에만 edge를 찾고 싶으면, 나머지 색은 모두 0으로 주면 된다
만약 여러 필터를 동시에 적용하고 싶으면, 따로 계산 후 결과 행렬의 채널을 늘리면 된다

channel 대신 depth라는 용어를 사용하기도 한다
One Layer of a Convolutional Network
CNN의 한 레이어를 살펴보자
앞서 GD에서와 비슷해서 필터(w)를 곱해 준 후 편향(b)을 더해주고, 활성화 함수에 넣어주어야 한다

필터가 기존의 feature가 된 느낌?
각 필터가 수직선, 수평선과 같은 특징을 뽑아내니 적절한 비유 같다
필터의 크기로 parameter 수가 정해지기에, 입력되는 이미지 크기가 변하더라도 변수의 수는 변하지 않는다
(\(n_H^{[l]}\times n_W^{[l]} \times n_c^{[l-1]} +1)\times n_c^{[l]}\) (+1은 bias)
이후에 사용할 표기법을 알아보자
\(f^{[l]}\) = filter size
\(p^{[l]}\) = padding
\(s^{[l]}\) = stride
\(n_c^{[l]}\) = number of filters
또한 변수들의 차원은 아래와 같다
Input : \(n_H^{[l-1]}\times n_W^{[l-1]}\times n_c^{[l-1]} \)
Output : \(n_H^{[l]}\times n_W^{[l]}\times n_c^{[l]} \)
Each filters : \(f^{[l]}\times f^{[l]} \times n_c^{[l-1]}\)
Activations : \(n_H^{[l]}\times n_W^{[l]}\times n_c^{[l]}\) or \(m \times n_H^{[l]}\times n_W^{[l]}\times n_c^{[l]}\)
Weights : \(f^{[l]}\times f^{[l]} \times n_c^{[l-1]}\times n_c^{[l]}\)
bias : \(n_c^{[l]}\); \((1,1,1,n_c^{[l]})\)
순서는 좀 달라질 수 있고, 구성은 대충 위와 같다 (높이, 너비, 채널 순서 바뀌는 느낌)
Simple Convolutional Network Example
레이어 수를 늘린 예시를 보자

시작 이미지에서 필터를 지나며 학습한다
마지막에 로지스틱 회귀 함수나, 소프트맥스 등을 통해 최종 판단을 한다
CNN에는 보통 3종류의 레이어가 존재한다
- Convlution (Conv)
- Pooling (Pool)
- Fully connected (FC)
지금 위에서 한 건 Conv 레이어다
Pooling Layers
pooling 레이어는 크기를 줄인다
정보를 압축하여 overfitting을 방지할 수 있다
(\f,s\)를 하이퍼 파라미터로 가지며, \((f=2,s=2)\)나 \((f=3,s=2)\)를 주로 사용한다고 한다
아래는 max pooling의 예시이다

\(f=2, s=2\) 인 풀링 필터를 적용했다
학습 가능한 파라미터가 없어 GD를 할 수 없다는 게 특징이다

max pooling이 보통 더 많이 사용된다고 한다
Fully-Connected layer
왜인지 이 레이어 강의가 없다
따로 찾아서 보자
FC는 CNN의 마지막에서 분류 등에 사용된다
모든 층의 뉴런이 다음 층의 뉴런에 연결되었기에 이름이 FC이다
다차원 배열을 1차 원로 flatten 하고, 활성 함수를 사용하는 일련의 과정을 수행한다

CNN Example
손글씨 인식 하기 문제를 살펴보자
LaNet-5라는 고전적인 신경망과 유사하게 구성한다
pool과 conv를 각각 하나의 레이어라고 보기도 하고, 가중치와 변수가 있는 레이어만 하나의 레이어라고 보기도 한다(뒤의 경우는 conv만 레이어)
뒤의 방식으로 표기하셨다

NN이 깊어질수록 \(n_H, n_W\)와 Activation size는 줄고, \(n_c\)는 줄어드는 경향을 보인다
conv-pool-conv-pool-fc-fc-fc-softmax
보통 위와 같은 형태를 이룬다
Why Convolutions?
그래서 CNN이 왜 잘 작동하는 걸까
두 가지 장점을 가진다
파라미터 공유 (Parameter sharing), 희소성 (sparity of connection)
각각 장점을 자세히 알아보자
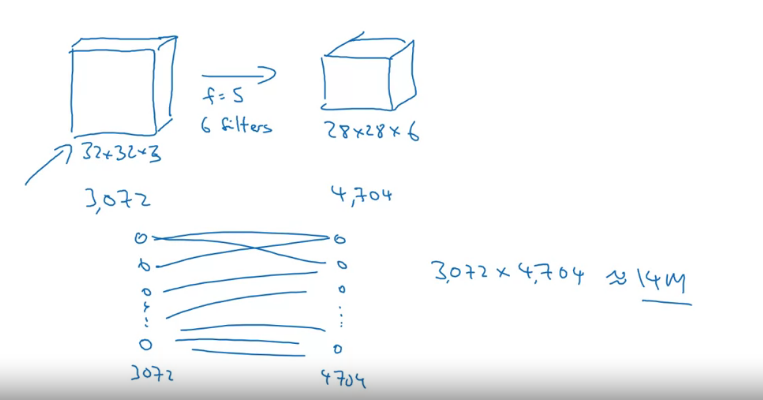
만약 이전처럼 모든 노드를 잇는 학습을 한다면 14000000개쯤의 어마어마한 수의 파라미터를 학습시켜야 한다
이미지가 작은데도 저렇게 많으면 커지면 감당이 안될 것이다
그러나 CNN에선 파라미터를 공유하기에 필터랑 26개, 126개의 파라미터만 학습시키면 된다
또한 각 레이어에서 출력 값은 적은 수의 input 특징의 영향을 받는다
필터에 해당하는 값들의 영향을 받기에 overfitting을 막을 수 있다
또한 조금 이동한 유사한 이미지 (고양이가 좀 움직이던가?)를 학습하는데 유리하다