Neural Networks and Deep Learning - 2 week
신경망 계산에선 for문 사용을 줄이는 게 좋다고 한다
왜인지는 모르겠으니 마법이라 생각하자
아마도 컴퓨터 시스템 개론에선 배운 레지스터와 무언가 관련이 있어 보이기도 하고, numpy에서 잘~ 구현을 해둔 걸 지도 모르겠다
아무튼 for문 사용을 줄이고, 메써드를 사용하자
또한 NN 구현에 사용되는 순전파(Forward Propagation)과 역전파(Backward Propagation)을 배워보자
Binary Classification
이미지를 보고 고양이인지 아닌지 판단하는 문제를 살펴보자
이에는 이진 분류가 사용된다
이진 분류는 고양이(1)인가 아닌가(0)처럼 두 가지로 분류하는 분류 알고리즘이다
이름 그대로 정직해서 마음에 든다
그런데 이진 분류에 사용되는 로지스틱 회귀(Logistic Regression)는 분류 알고리즘이면서 Regression이 들어간다. 헷갈리지 않도록 하자
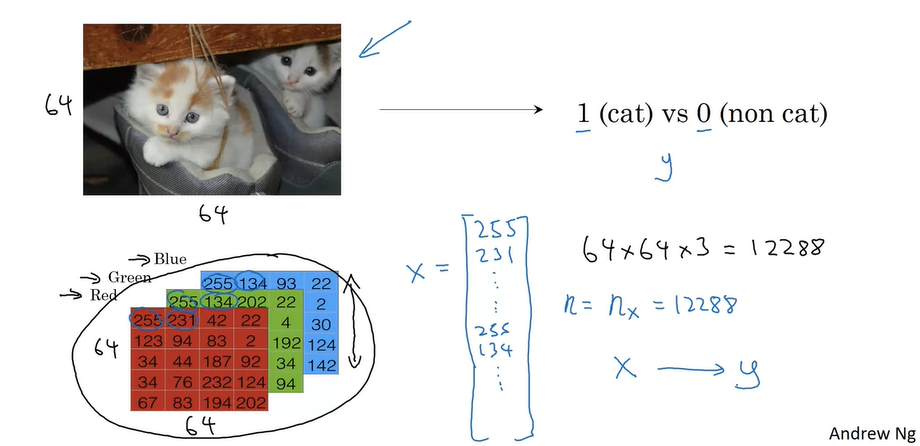
컴퓨터는 이미지를 RGB 데이터를 픽셀 별로 인식한다
64*64의 3개 행렬을 하나의 column vector로 만들면 12288차원의 벡터이다
이 \(n_x=122\,88\) 의 크기를 가지는 X가 입력값이다
\(n_x\)가 등장했는데, 앞으로 볼 이런저런 표기법(Notation)을 짚고 넘어가자
- \(\begin{matrix}(x, y) & x \in \mathbb{R}^{n_x}, y \in \{0, 1\}\end{matrix}\) : example 하나를 나타낸다.
- \(m\) trainig example : \({ ( x^{(1)},y^{(1)}), \cdots,( x^{(m)},y^{(m)})}\)
- \(X=\begin{bmatrix}
|& |& & | \\
x^{(1)} & x^{(2)} & \cdots & x^{(m)} \\
|& |& & | \\
\end{bmatrix}\) - 출력 \(Y\)\((Y \in \mathbb{R}^{1 \times m}\)은 row vector이다
\(Y=\begin{bmatrix}
y^{(1)} & y^{(2)} & \cdots & y^{(m)} \\
\end{bmatrix}\)
LaTex 쓰기 너무 힘들었다. 이뻐서 뿌듯하다. 칭찬해 주시길 바란다.
Logistic Regression
로지스틱 회귀면서 이진 분류에 사용되는 알고리즘이다
우리는 입력 \(x\)가 주어졌을 때, \(\hat{y} = P(y=1|x)\)를 구하고 싶다
\(\hat{y}\) 이 모자를 쓴 친구는 y hat 이라고 읽으며 추정치를 의미한다
우리의 output은 \(\hat{y} = \sigma(w^{(T)}x + b)\)로 나타난다
시그마는 시그모이드 함수로 아래와 같이 생겼다

시그모이드의 식은 아래와 같다
\(\sigma(z)= {1\over{1+e^{-z}}}\)
양쪽 극한으로 가면 기울기의 절댓값은 0으로 수렴하게 된다
0과 1 사이에 출력 값을 위치시키기 위해 시그모이드 함수를 사용한다
Logistic Regression Cost Function
우리의 목적은 최적의 parameter(\(w, b\))를 찾는 것이다
그렇기에 현재 예측이 얼마나 정확한지를 알아야 한다
이를 Loss Function과 Cost Fuction(비용 함수)를 이용하여 구한다
Loss Function은 하나의 예제의 오차이다
\(\mathcal{L}(\hat{y}, y) = {1\over 2}(\hat{y}-y)^2\)
위와 같은 식은 non-convex하여 Local optima에 빠질 수 있다. 그렇기에 새로운 convex한 loss를 정의하자
\(\mathcal{L}(\hat{y}, y) = -(ylog(\hat{y})+(1-y)log(1-\hat{y}))\)
왜 식이 이렇게 되는지는 마법이라 생각하자
이를 모든 예제에 대해 sum 하면 비용 함수를 구할 수 있다
\begin{align*}
\mathcal{J}(w,b)&={1\over m} \sum_{i=1}^{m}\mathcal{L}(\hat{y^{(i)}}, y^{(i)})\\
&= -{1\over m} \sum_{i=1}^{m}[(y^{(i)}log(\hat{y^{(i)}})+(1-y^{(i)})log(1-\hat{y^{(i)}}))]
\end{align*}
Gradient Descent
경사 하강 알고리즘을 이용하여, 매개변수 w, b를 학습시켜서 비용 함수를 최소화하는 것이 목표다

비용 함수는 convex하므로 임의의 아무 점에서 경사 하강을 이용하여 global optim에 도달 가능하다
convex 한 것도 마법이다
\(w=w-\alpha {d\mathcal{J}(w,b)\over dw}\)
\(b=b-\alpha {d\mathcal{J}(w,b)\over db}\)
위 두 식을 반복하여 구현 가능하다
파이썬 구현은 아래서 살펴보자
Derivatives, More Derivative Examples
미분을 잘해 낸다
미적분학 수업에서 들어 아는 내용이니 넘어가자
Computation Graph
계산 과정을 그래프로 나타낸 것이다


Derivatives with a Computation Graph
다음으로 오른쪽에서 왼쪽으로 가며 Chain rule을 사용하여 각 값의 미분을 구할 수 있다.
\(d\mathcal{J}\over dv\)와 같은 표기법은 너무 길기에 \(dv\)라고 표기해 주자
현재에 대해 각 값을 계산해 주면 아래와 같다(오른쪽부터 계산하자)
| \(dv = 3\) \(du = dv\times {dv\over du} = 3\) \(da = dv\times {dv\over da} = 3\) \(db = du\times {du\over db} = 6\) \(dc = du\times {du\over dc} = 9\) |
미분의 고수라 잘할 수 있으리라 믿는다
Logistic Regression Gradient Descent
| \(z=w^{T}x+b\) \(\hat{y}=a=\sigma(z)\) \(\mathcal{L}(a, y) = -(ylog(a)+(1-y)log(1-a))\) |
위 변수들로 계산 그래프를 그려보자

잘~ 미분을 하면 다음과 같은 식들을 유도할 수 있다.
이 마법들은 검색하면 쉽게 찾을 수 있다
| \(da=-{y\over a}+{1-y\over1-a}\) \(dz=a-y\) \(dw=xdz\) \(db=dz\) |
위 식들은 기억해 두자
또한
\(sigmoid(p)=q\)라고 하면, \({dq\over dp}=q(q-q)\) 이다
Gradient Descent on m Examples
위는 한 개의 예제에 대한 미분이고, m개에 대한 미분을 알아보자
우리는 모든 example에서 경사 하강법을 적용해야 한다
따라서 위 첨자 i를 추가하여 식을 다음과 같이 바꾸자
| \(z^{(i)}=w^{T}x^{(i)}+b\) \(\hat{y^{(i)}}=a^{(i)}=\sigma(z^{(i)})\) \(\mathcal{L}(a^{(i)}, y^{(i)}) = -(y^{(i)}log(a^{(i)})+(1-y^{(i)})log(1-a^{(i)}))\) |
각각 example에서 \({dw_1}^{(i)}, {dw_2}^{(i)}, {db}^{(i)}\)를 계산 가능하다
또한 비용 함수는 아래와 같이 표현된다
\(\mathcal{J}(w,b)={1\over m} \sum_{i=1}^{m}\mathcal{L}(\hat{y^{(i)}}, y^{(i)})\)
이를 \(dw_1\)으로 미분하면 다음과 같다
\({d\over dw_1} \mathcal{J}(w,b)={1\over m} \sum_{i=1}^{m} {d\over dw_1}\mathcal{L}(\hat{y^{(i)}}, y^{(i)})\)
즉 \({dw_1}^{(i)}\)의 평균이다
경사 하강을 코드로 나타내면 다음과 같다
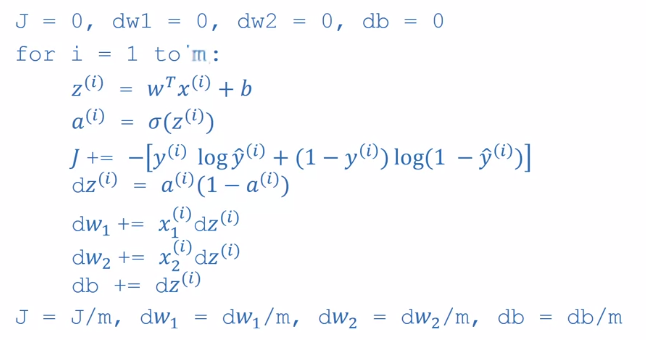
계산 후, 변수를 업데이트해준다

그러나 이 과정에선 슬프게도 사용을 최소화해야 할 for문이 이용된다
이는 numpy 함수들을 이용하여 개선 가능하다
Vectorization~~
넘 파이 등 사용법을 잘 익히자
파이썬은 너무나 친절하여 자기 맘대로 브로드캐스팅을 하기에 버그에 유의 하자
for문 사용보다 내장 함수 사용이 무조건 유리하다
변수 이름을 잘 보자..
param인지 pram인지 오타를 내면 1시간이 사라진다.. 😥😥