Neural Networks and Deep Learning - 3 week
Neural Networks Overview
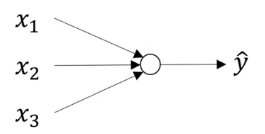
지금까지 단일 레이어 신경망을 살펴보았다
이번 주차에는 여러 층으로 구성된 신경망을 구성하는 법을 알아볼 것이다
Neural Network Representation
먼저 표기법들을 알아보자
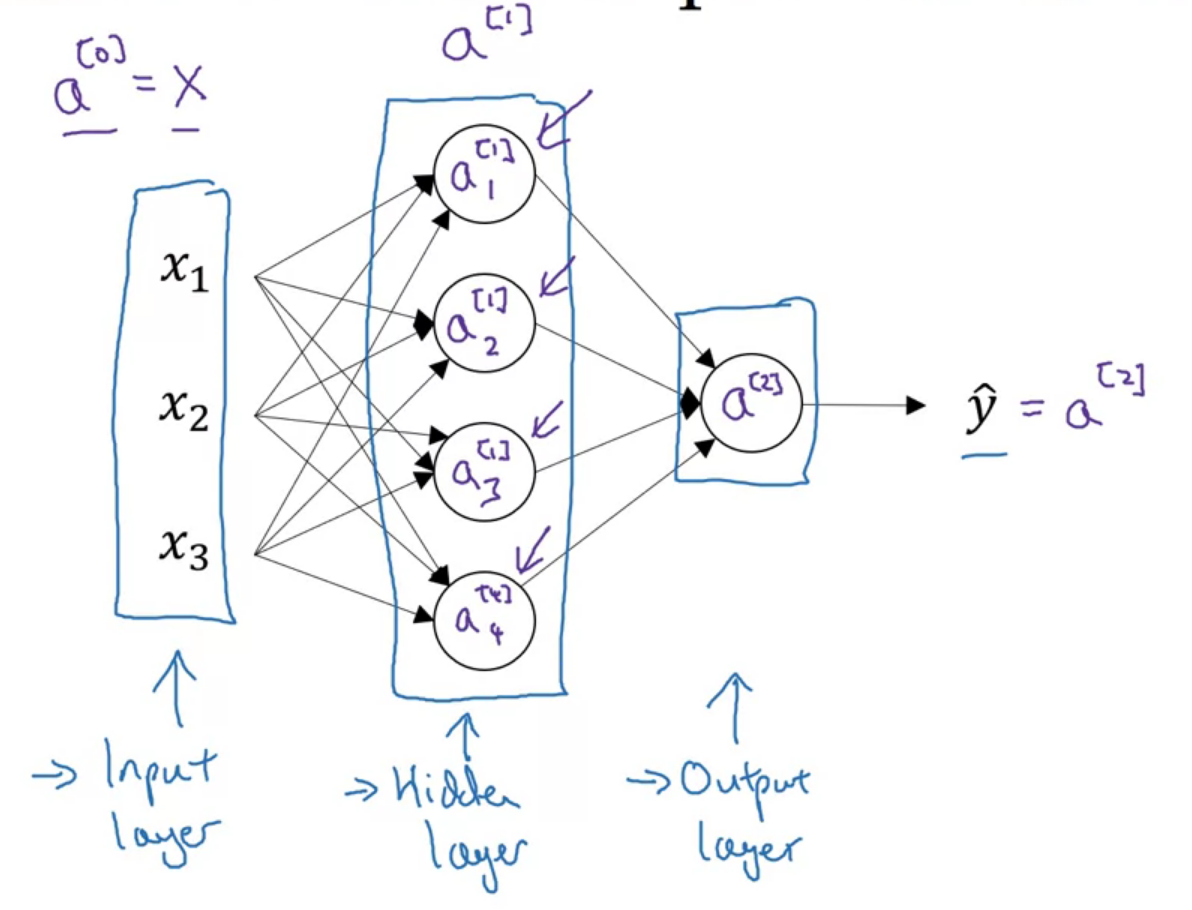
입력 레이어를 input layer, 출력 레이어를 output layer라고 한다
또한 학습 세트 중간에서 노드의 실제 값이 관찰되지 않는 층들을 hidden layer라고 한다
| \(L\) : Number of total layer \(n^{[l]}\) : number of units of later \(l\) \(a^{[l]}\) : Activations of layer \(l\), \(a^{[l]}=g^{[l]}(z^{[l]})\) \(w^{[l]}\) : weights for \(z^{[l]}\) \(b^{[l]}\) : bias parameter for \(z^{[l]}\) |
아래 첨자는 몇 번째 노드인지를 가르킨다
위 첨자 (i)는 몇 번째 example인지 나타낸다
Input layer은 \(a^{[0]}\)이다
위의 신경망의 경우 \(L=4, a^{1}=4\) 이다
Computing a Neural Network's Output

하나의 노드를 계산하는 과정이다 (FP)
신경망의 각 노드에선 해당하는 계산이 일어난다

각 노드에선 다음과 같은 계산이 일어난다
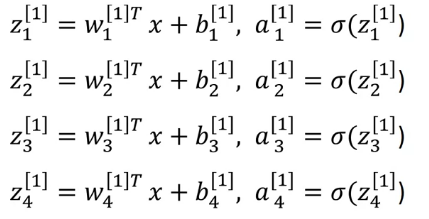
동일한 반복이니 for문을 이용해 구현한 수 있지 않을까 라는 생각이 든다
그러나 앞서 배운 것처럼 명시적 for문을 최소화해야 한다
for문 대신 행렬 연산을 사용하는 것이 시간 면에서 더 이득이 된다.
하나의 예제에 대해 일반화하면 다음과 같다
| \(z^{[l]}=w^{[l]}a^{[l]}+b^{[l]}\) \(a^{[l]}=g^{[l]}(z^{[l]})\) |
그리고 이를 모든 학습 예제에 대해 벡터화하면 다음과 같이 표기할 수 있다
| \(Z^{[l]}=W^{[l]}A^{[l]}+b^{[l]}\) \(A^{[l]}=g^{[l]}(Z^{[l]})\) |
파이썬으로 구현하며 행렬의 차원을 잘 고려하자
Vectorizing Across Multiple Examples
행렬은 column vector(각 training example에 대한 벡터)를 쌓아서 형성된다
\(Z^{[l]}=\begin{bmatrix}
|& |& & | \\
Z^{[l](1)} & Z^{[l](2)} & \cdots & Z^{[l](m)} \\
|& |& & | \\
\end{bmatrix}\)
Explanation for Vectorized Implementation
구현을 잘 하자
Activation Functions
hidden layer에 어떤 활성화 함수를 사용해야 할까
활성화 함수는 Z값에 적용시켜 출력신호로 변환시키는 함수이다
activation function이라 지금까지 A를 사용했다
sigmoid나 이름이 귀여운 ReLU 등이 활성화 함수이다
보통 tanh 함수가 평균이 0이기에 시그모이드 보다 잘 작동한다
sigmoid를 shift 시킨 것뿐인데 잘 작동되는 이유는 뭘까?
일단 마법이라 생각하고 넘어가자
그러나 이진 분류의 경우 값을 0~1 사이에 위치시켜야 하기에 마지막 레이어에 시그모이드를 적용시키자
시그모이드와 tanh의 단점은 값의 절댓값이 커짐에 따라 기울기가 0으로 수렴한다
즉 큰 값에서 수렴까지 오랜 시간이 걸려, 학습 시간이 길어진다
그러므로 렐루를 쓰자
이름도 시그모이드 보다 3.27 배 정도 귀엽고, 기울기가 큰 값에 대해 매우 작아지는 문제가 발생하지 않는다

잘 모르겠으면 이진 분류를 시그모이드, hidden layer에는 렐루를 쓰자
무엇을 선택할지 모르겠으면 일단 다 적용시켜보고 가장 나은걸 선택하자
Why do you need Non-Linear Activation Functions?
이름이 귀여운 함수들을 쓰는 이유는 무엇일까?
그냥 선형 함수를 쓰면 안 되는 걸까?
정답을 먼저 보자면 아무래도 잘 사용하지 않는다
y=x라는 선형 함수를 활성화 함수로 사용한다고 해보자
| \begin{align*} a^{[2]} &= w^{[2]}a^{[1]}+b^{[2]}\\ &=w^{[2]}w^{[1]}x + w^{[2]}b^{[1]}+b^{[2]} \\ &=w^{'}x+w^{'} \end{align*} |
2-layer NN이지만 마치 단일 층인 것처럼 동작한다
즉 여러 layer해도 의미가 없다
그러나 regression의 경우 실수 범위의 값을 얻어야 하기 때문에 선형 활성 함수를 사용하기도 한다
Derivatives of Activation Functions
위의 4개의 활성 함수를 미분하면 아래와 같다
- 시그모이드
\(g(z)={1\over {1+e^{-z}}}\)
\(g^{'}(z)=g(z)(1-g(z))\) - tanh
\(g(z)={{e^{z}-e^{-z}}\over {e^{z}+e^{-z}}}\)
\(g^{'}(z)=1-g^{2}(z)\) - ReLU
\(g(z)=\max (0,z)\)
\(g^{'}(z)=\begin{cases}
0& \text{ if } z<0 \\
1& \text{ if } z>=0
\end{cases}\) - Leaky ReLU
\(g(z)=\max (0.01z,z)\)
\(g^{'}(z)=\begin{cases}
0.01& \text{ if } z<0 \\
1& \text{ if } z>=0
\end{cases}\)
Gradient Descent for Neural Networks
신경망의 경사 하강법도 앞서 본 것과 크게 다르지 않다
FP로 비용 함수를 구하고, BP를 하며 미분을 구하고, 변수 값을 업데이트한다
각 값을 일반화하면 아래와 같다
| \(da^{[l]}={d\mathcal{L}\over da^{[l]}}\) \(dz^{[l]}=da^{[l]}\times g^{' [l]}(z)\) \(db^{[l]}=dz^{[l]}\) \(dw^{[l]}=dz^{[l]}\times a^{[l-1]}\) |
만약 train exaple이 여러 개라면, sum 하고 1/m 곱해주면 된다
Random Initialization
NN의 파라미터 w, b를 초기화할 때, w는 랜덤 한 값으로 초기화해야 한다
만약 w가 동일하다면 dz가 동일하게 되고, 각 노드는 동일하게 된다
따라서 임의 초기화 해야 한다
작은 값으로 초기화하는데, 시그모이드, 하이퍼볼릭 탄젠트 도함수를 작게 만들기 위해서다
잘 모르겠으면 그냥 마법으로 생각하고
w->0 근처 값으로 랜덤, b 그냥 0으로 초기화라 생각하자