Convolutional Neural Networks - 4 week

CNN의 마지막 주차에선 몇몇 응용 프로그램을 알아볼 것이다

얼굴 인식, neuron tranfer 같은 걸 배워보자~

What is Face Recognition?

예시로 실제 사용 영상을 보여주셨다

id 카드 없이 얼굴 인식으로 게이트를 통과한다

신기하게도 id 카드의 사진으론 통과를 시키지 않는다 (사진 카메라에 보여줘도)

 

간단히 용어를 좀 짚고 넘어가자

Face verification과 face recognition이라는 두 가지 문제가 있다

	Face verification	Face recognition
input	image, name/ID	image (hase data base)
output	whether input image is that of claimed person or not	ID if image is any of person in db or not recognized

Verification이 입력과 1 : 1로 비교라면, recognition은 DB의 K 개의 데이터와의 1 : K 비교이다

따라서 보통 recognition이 좀 더 어렵다

verification 위주로 공부해 보자

One Shot Learning

얼굴 인식을 하기 위해선 one shot learning problem을 해결해야 한다

다시 말해 하나의 이미지나, example로 얼굴을 인식 해야한다

ID 등록 과정에서, 프로필 이미지 100만 장을 제출하시오 (얼굴 각도, 다양한 옷 입고.. 등등)라고 하면, 아무도 사용하지 않을 것이다

 

뭔가 각각 이미지를 CNN에 넣어 softmax를 시키면 인식을 간단히 할 수 있지 않을까?라는 생각이 드는데

너무나 아쉽지만 training set이 너무 작기에 잘 작동하지 않는다

또 DB에 사람이 추가된다면, softmax의 출력 수를 계속 늘려야 하는 문제도 있을 것이다

 

similarity function을 이용하여 이를 해결할 수 있다

아래와 같은 느낌으로 작용한다

d(img1, img2) = degree of difference between images

 threshold처럼 일정 값을 기준으로 같다, 다르다를 판단하면 된다

DB 4가지 이미지에 각각 d를 구한다

만약 이미지가 DB에 없다면 모든 이미지에 대해 큰 값이 나와, DB에 없다고 출력할 것이다

Siamese Network

얼굴의 유사도를 알려주면 d를 알려주는 방법 중에는 siamese Net이 있다

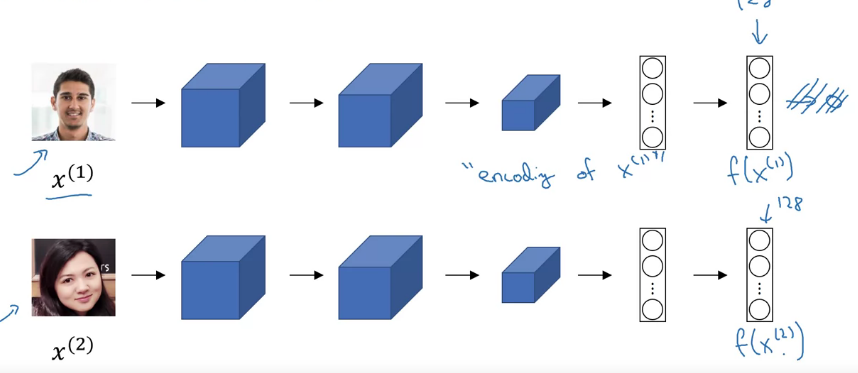
이제는 익숙한 conv net

CNN을 통해 각각의 이미지 \(X^{(i)}\)를 f로 encoding 해 준다

d를 계산하기 위래 두 이미지 사이를 아래와 같이 정의하자

\(d(x^{(1)},x^{(2)}) = \|f(x^{(1)})-f(x^{(2)})\|^2_2\)

이렇게 동일한 conv로 f 벡터를 얻고 값을 비교하는 것을 siamese architecture라고 한다

Triplet Loss

siamese 아키텍처를 잘 작동하기 위한 로스 함수, Triplet loss에 대해 배워보자

삼중항 손실은 이미지 쌍에서 정의된다

anchor 이미지(우리가 가진 한 장)로부터 positive(동일한 사람)인지 negative(다른 사람)인지 판단해야 한다

위에서 처럼 3가지 이미지를 동시에 보기에 용어 이름이 그렇다

각각을 A, P, N 으로 부르자

우리가 원하는 바는 아래 조건을 만족하는 것이다

\(d(A,P) \leq d(A, N)\)
\(\|f(A)-f(P)\|^2_2 \leq \|f(A)-f(N)\|^2_2\)

\(\|f(A)-f(P)\|^2_2 - \|f(A)-f(N)\|^2_2 \leq 0\)

만약 f가 모든 이미지에 대해 동일하거나, 0이면 방정식이 참이다

그렇기에 모든 인코딩이 서로 동일하게 설명되지 않아야 한다

그렇기에 좌변에 작은 값 \(\alpha\) (margin)을 더해주어서 이 문제를 해결한다

SVM에서 본 것과 비슷한 느낌이라고 한다

식과 로스를 쓰면 아래와 같다

\(\|f(A)-f(P)\|^2_2+\alpha \leq \|f(A)-f(N)\|^2_2\)
\(\|f(A)-f(P)\|^2_2 - \|f(A)-f(N)\|^2_2 +\alpha \leq 0\)

\(\mathcal{L}(A, P, N) = \max(\|f(A)-f(P)\|^2_2 - \|f(A)-f(N)\|^2_2 +\alpha, 0)\)
\(\mathcal{J}=\sum_{i=1}^{m}\mathcal{L}(A^{(i)}, P^{(i)}, N^{(i)})\)

기존 식에서 0 이하이기 때문에 max를 취해준다

목표를 달성한다면 0을 가지게 된다

 

A, P는 동일한 사람이어야 하기에 동일한 사람 사진이 여러 개 있는 훈련 세트가 필요하다

물론 학습 후에는 하나만 있으면 된다

 

A, P, N을 선택하는데 주의가 필요하다

만약 무작위로 선택을 하면, 당연히 A와 P 사이의 차이점보다 A와 N 사이의 차이점이 클 확률이 높다

 

그렇기에 학습하기 힘들도록 "잘" 선택해야 한다

그러다 보면 d(A, P)와 d(A, N)이 비슷한 값을 가지는데, 전자를 줄이던가 후자를 키워 모델을 잘 작동하게 만들어야 한다

Face Net 논문을 찾아보면 나와있다고 한다 (마법이구나)

 

 

그리고 갑자기 명명법? 같은걸 알려주셨다

___ Net, Deep ___ 식으로 부르는 게 인기? 유행이라고 한다

이번에 배운건 얼굴이므로 Face Net, Deep Face인 느낌

Face Verification and Binary Classification

이진 분류로 얼굴 인증 문제를 다룰 수 있다고 한다

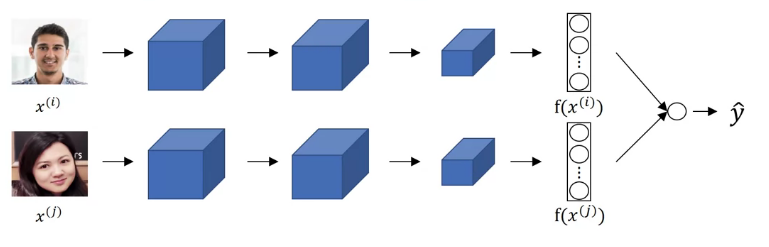
아키텍쳐의 출력 값을 로지스틱 단위에 입력한다

물론 \(\hat{y}\)은 두 encoding 사이의 차이를 알아야 하기에 아래와 같은 형태가 되어야 한다

\(\hat{y} = \sigma (\sum_{k=1}^{128} w_k | f(x^{(i)})_k - f(x^{(j)})_k| +b )\)

128은 아키텍처 출력 벡터 차원을 128로 생각해서 그렇다

차이를 계산하여 카이 제곱 유사도와 같은 다른 유사도 항을 사용해도 무관하다

 

DB에 있는 값들은 미리 계산하여 전처리해두면 시간 절약을 할 수 있다

 

 

What is Neural Style Transfer?

conv net에서 흥미로운 애플리케이션 중 하나는 Neural style transfer이라고 한다

어디서 많이 본 그림 스타일 바꾸기? 기능이다

C의 내용을 S에서 스타일만 받아와 G를 생성한다

What are deep ConvNets learning?

심층 convNet 학습이 뭔지 알아보자

딥러닝을 시각화하여 직관을 알아보자

히든 유닛이 무엇을 의미하는지 알아내기 위해

이런저런 이미지를 input으로 집어넣어보며, 해당 유닛의 활성화를 최대화하는 입력을 찾아보자

예를 들어 아래와 같은 최대화시키는 9개의 이미지를 찾아 패치로 만든다

이걸 보고 아 이 유닛은 모서리 선 같은 걸 찾나 보구나~ 알 수 있다

다른 유닛에 대해 반복하자

초록색을 좋아하는 친구, 주황색을 좋아하는 친구, 대각선 등등 대충 보인다

이를 다른 레이어들에도 반복하자

작긴한데 참고 보자

레이어가 깊어질수록, 단순한 선과 색을 넘어 더 복잡한 형태와 객체를 인식하고 있다

Cost Function

Neural style transfer 시스템 구축을 위한 이미지 비용 함수 정의를 알아보자

생성된 이미지 G의 비용 함수를 살펴볼 것이다

두 이미지를 합쳤으므로, 직관적으로 두 이미지 모두와 비슷해야 할 것 같다

그러므로 두 가지 항을 모두 계산해야 한다

비율을 따지기에, 하이퍼 파라미터를 곱해준다 (하나만 있어도 되지만, 원저자가 두 개를 써서 알파, 베타를 모두 사용한다)

\(\mathcal{J}(G) = \alpha \mathcal{J}_{content}(C,G) + \beta \mathcal{J}_{style}(S,G)\)

이미지를 랜덤으로 생성하고, 경사 하강법을 반복한다

그러면 노이즈에서 원하는 이미지를 점점 얻을 수 있다고 한다

각각 Cost Function을 어떻게 정의하는지 배워보자

Content Cost Function

히든 레이어 \(l\) 번을 사용하여 content cost를 계산한다

너무 얕지도, 깊지도 않아야 한다고 한다 (당연한 거.. 아닌가요 교수님..?)

VGG net과 같은 pre-trained convnet을 사용하라고 하신다

레이어 \(l\)의 activation \(a^{[l](C)}\), \(a^{[l](G)}\)를 비교하여 비슷한지 판단한다

\(\mathcal{J}_{content}(C,G) = \| (a^{[l](C)} - (a^{[l](G)}\|^2\)

정규화 상수 1/2 같은 건 어차피 \(\alpha\)로 조정하니 생략했다

결국 content cost를 줄이는 것은 원본 이미지와의 유사도를 높이는 일이다

Style Cost Function

다음으로 style cost function을 알아보자

style을 한 활성에서 채널 사이의 correlation(상관관계)라고 정의하자

그래서 상관관계가 뭐냐고?

상관 관계가 높다는 것은, 특정 \(n_W, n_H\) 사이의 연관성이 높다는 의미이다

 

예를 들어 빨강과 노랑 채널 사이의 상관관계가 높다면, 수직선이 있다면 주황색으로 나타난다

즉 높은 단계의 특징에 대해, 얼마나 같이 발생하는지를 측정하는 게 style을 알아내는 것이다

 

수식을 통해 알아보자

\((i, j, k)\)에서의 활성을 \(a_{i, j, k}^{[l]}\)이라고 하자 (순서대로 H, W , C 차원이다)

우리는 먼저 \(k\)와 \(k^{'}\) 채널 사이의 \(G^{[l]}_{kk^{'}}\)을 구해야 한다(\G^{[l]}\)의 차원은 \(n_c^{[l]}\times n_c^{[l]}\)이다)

(G는 Gram matrix에서 온 문자이다)

\(G^{[l]}_{kk^{'}} = \sum_{i=1}^{n^{[l]}_H}\sum_{j=1}^{n_W^{[l]}}a_{ijk}^{[l]}a_{ijk^{'}}^{[l]}\)

두 항이 correlation을 가지면, G 값이 커지고 아니면 작아질 것이다

사실 표준편차로 나눠주지 않고, 곱하기만 하기에 엄밀하게 상관관계는 아니지만 그러려니~ 하자

 

위 계산을 생성된 이미지와 스타일 이미지 모두에 시행하여, 아래와 같은 cost function을 구할 수 있다

글씨가 깨지니 캡처로 보자

위의 시그마 식은 S와 G 사이의 Frobenius norm으로부터 왔다

전체 style cost function은 아래와 같다

\( \mathcal {J}_{style}(S, G) = \sum_l \lambda^{[l]} \mathcal {J}_{style}^{[l]}(S, G)\)

낮은 레벨과 높은 레벨의 특징을 모두 스타일에 고려하게 만들었다

 

자 이제 cost function 구성은 모두 배웠다!

1D and 3D Generalizations

지금까지 convnet에 대해 다양하게 배웠다

지금까지는 2D에 대해서 배웠지만, 사실 3D와 1D에서도 잘 작동한다

2D 처럼 1D에 적용하자

왼쪽의 신호는 심전도 신호이다

여기에 1차원 필터를 곱하여 결과를 얻는다

 

3차원 이미지는 CT 스캔과 같은 이미지다

마찬가지로 차원에 맞는 필터를 곱해 값을 얻어낸다

 

차원이 달라져도 앞에 내용과 거의 유사하니 넘어가자