Sequence Models - 1 week

Why Sequence Models?

드디어 마지막 미션이다

딥러닝의 흥미로운 분야 중 하나인 RNN (Recurrent Neural Network) 모델을 배워 볼 것이다

sequential model의 적용 예시를 몇 가지 알아보자

연속적인 무언가

입력과 출력 모두 시퀀스 일 수도 있고, 둘 중 하나만 시퀀스 일 수도 있다

Notation

Name entity 인식 문제 예제를 통해 알아보자

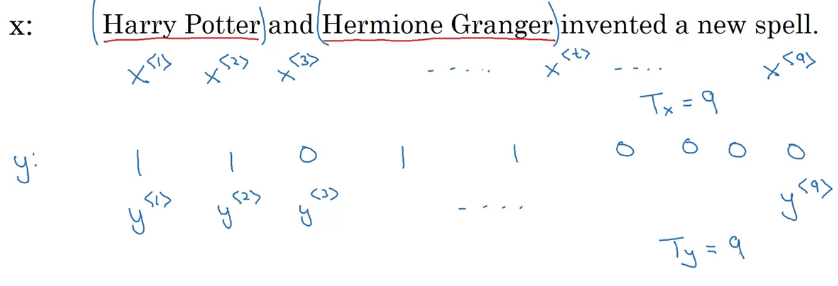
입력 시퀀스는 단어의 나열이다

각 단어를 위 첨자 < >을 통해 \(x^{<t>}\)로 나타낸다

스퀀스의 길이는 \(T_x, T_y\)로 나타낸다

이 예제에선 둘이 같지만, 다를 수도 있다

다른 표기와 함께 사용하여 \(x^{(i)<i>}\) i 번 예제의, t 번 시퀀스와 같은 표기를 할 수 있다

 

NPL에선 사용할 단어 목록을 먼저 만들어야 한다

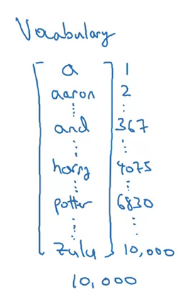
큰 어플리케이션은 단어가 더 많다

보통 사전은 빈도수 상위 단어처럼 많이 등장하는 단어를 채워 넣는다

그리고 one-hot을 통해 각각을 찾는다 (다른 모든 값 0, 해당 수만 1)

즉 이름 찾기 문제는 one-hot input vector x를 y로 지도 학습시키는 것이다

Recurrent Neural Network Model

자자 표기법도 알았으니 모델 구조 살펴보자

먼저 기존 모델을 그냥 사용 한다면 몇몇 문제가 발생한다

단어 위치를 노드로 하는 모델을 만든다면 뭔가 이상하다

먼저 입출력 개수가 달라지는 문제가 발생할 수 있다

당연히 문장 길이가 달라진다면 개수도 달라질 것이다

또한 학습된 feature를 공유하지 않는다

세 번째 등장한 Harry는 사람 이름일 것이다! 라는 추론보단

가만 보니 Harry는 보통 사람 이름이더라가 뭔가 합리적으로 보인다

(위치에 따른 특징이 아니다!)

 

이를 해결하기 위해 RNN을 배워보자

왼쪽에서 오른쪽으로 문장을 읽고, 첫 번째 단어를 \(x^{<1>}\)라고 하자

\(x^{<1>}\)를 NN에 넣어 예측 값 \(\hat{y}^{<1>}\)을 구한다

그리고 다음 \(x^{<2>}\)로 반복한다

그런데 RNN은 첫 \(x^{<1>}\)의 예측에 사용된 \(a^{<1>}\)를 \(x^{<2>}\) 계산에 사용한다

즉 이건 예측 값을 사용하여, 현재 예측에 추가적인 정보로 사용한다

편의상 입출력 크기가 같다구 했다 (다르면 아키텍처 일부가 변형된다)

보통 첫 입력에는 \(a^{<1>}\)를 널벡터로 사용하지만, 일부 연구에선 랜덤 초기화 값을 사용하기도 한다

이렇게 순환을 표기하기도 한다

각 반복 과정에서 동일한 매개변수가 사용된다

수식으로 보면 아래와 같다

\(a^{<t>} = g(W_{aa}a^{<t-1>} + W_{ax} x^{<t>} + b_a)\)
\(\hat{y}^{<t>}=g(W_{ya}a^{<t>} +b_y)\)

표기법을 단순화 하면 아래와 같이 변한다

\(a^{<t>} = g(W_{a}[a^{<t-1>},x^{<t>}] + b_a)\)
\(\hat{y}^{<t>}=g(W_{y}a^{<t>} +b_y)\)

RNN의 약점 중 하나는, 앞서 계산한 값들만 보고 현재 값을 계산한다는 것이다

처음 이름이 나온다면 Teddy가 사람의 일부인지 Teddy bear인지 알기 어려운 느낌이다

이를 양방향 RNN, BRNN같은 걸로 해결한다고 하긴 하는데 넘어가자

Backpropagation Through Time

구조는 알겠으니, BP 과정을 알아보자

사실 프레임워크에서 대부분 다 해주지만, 과정을 알고 있으면 유용하다고 한다

순서대로 쭉 FP를 시킨다

그리고 Loss를 구하는데, 로지스틱 로스를 사용할 것이다

각 시퀀스의 로스를 합치면, 전체 로스를 구할 수 있다

\(\mathcal{L}^{<t>}(\hat{y}^{<t>}, y^{<t>}) = -y^{<t>}log\hat{y}^{<t>}-(1-y^{<t>})log(1-\hat{y}^{<t>})\)
\(\mathcal{L}^{<t>}(\hat{y}, y)=\sum_{t=1}^{T_y}\mathcal{L}^{<t>}(\hat{y}^{<t>}, y^{<t>})\)

빨간 화살표가 BP 과정이다

동그라미 친 화살표가 가장 중요하다고 하며, BackPropagation Through Time(BPTT)라는 멋진 이름으로 부른다고 한다

Different Types of RNNs

초반 예시에서 입출력이 다양하고, \(T_x, T_y\)가 다를 수도 있다는 걸 알았다

위에서 알아본 \(T_x = T_y\)인 경우를 출력 시퀀스만큼 입력 값이 많고, 입력도 마찬가지기에 many-to-many 아키텍처라고 한다

 

긍정 or 부정 감정 분류 예제를 살펴보자

입력 x는 문장과 같은 text이고, 출력 y는 0 or 1 이 될 것이다

many-to-one

 

이렇게 출력이 하나인 경우, many-to-one 아키텍처라고 한다

one-to-one

물론 위와 같은 one-to-one 아키텍처도 있지만, 좀 단순해서 재미가 없다

 

one-to-many 아키텍처의 예시는 음악 생성기가 있다

입력은 첫 음이나, random seed나 그냥 null 일 수도 있다

출력은 만들어진 음의 박자, 높이 등등이다

출력 값을 다음 레이어에 전달하는 것도 다음에 배울 거니 추가하자

one-to-many

many-to-mant에서 입력과 출력 길이가 다른 경우는 어떻게 아키텍처를 구성해야 할까

번역과 같은 경우 각 언어에서 문장 길이가 다를 수도 있다

many-to-many

위와 같은 아키텍처를 사용하면, 입출력 수가 다른 경우에도 작동할 수 있다

Language Model and Sequence Generation

RNN을 이용한 언어 처리 모델을 알아보자

언어 인식 모델을 만들면, 발음이 비슷한 단어가 있을 수 있다

The apple and pair salad
The apple and pear salad

pair/pear과 같이 발음이 비슷한 단어에서, 음성 인식이 잘 작동한다면 아마도 첫 단어를 선택해야 한다

모델은 해당 문장이 선택될 가능성을 계산하고 선택한다

가능성은 해당 문장이 자연스러울 확률을 나타내는 느낌이다

 

모델의 입력을 알아보자

Training set은 큰 영어 텍스트 뭉치이다

이 문장들은 먼저 토큰화가 되어야 한다

토큰화는 각 단어를 one-hot vector로 매핑하는 것을 의미한다

문장의 끝에 <EOS> (end of setence) 토큰을 추가하곤 한다

마지막 마침표나 문장 부호도 토큰으로 만들기도 한다 (optional)

단어 사전에 없는 단어가 등장한다면 UKW(unknown) 토큰 등으로 배치하면 된다

 

다음으로 아키텍처를 알아보자

각 출력 값은 입력이 \(x^{<t>}\) 일 때, 각 단어가 다음에 등장할 확률이다

그렇기에 (x^{<t>}==y^{<t-1>}\)이다.

다시 말하자면 \(\hat {y}^{<t>}\)은 <t-1> 시퀀스까지 봤을 때 해당 단어가 등장할 조건부 확률이다

그림은 아래에 있으니 보도록 하자

 

다음으로 cost function은 아래와 같다

Sampling Novel Sequences

시퀀스 모델 학습 후, 문장의 예시는 sample novel sequence를 통해 알 수 있다

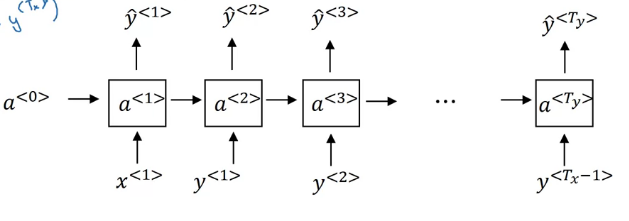
학습은 위와 같은 아키텍처를 사용한다

그러나 샘플링에는 조금 방식이 달라진다

np.random 등을 통해 단어를 무작위로 선택하고 넘어간다

 

모델은 단어가 아니라 Character-level 언어로 구성할 수도 있다

vocabulart = [a, b, c,..., 0, 1, 2,...,.,!,?,..., A, B, C...] 느낌으로

UNK에 대한 문제가 줄어들들지만, 출력의 길이가 길어지는 문제가 있다

또한 많은 계산 비용이 필요하다

그래도 성능이 좋아짐에 따라 문자 레벨 모델이 점점 더 많이 보인다고 하신다

Vanishing Gradients with RNNs

RNN 모델은 기울기 소실 문제를 가지고 있다

문장이 올바르기 위해선 맞출 조건이 많은데, 시제를 예시로 보자

먼 과거에, 근데 이제 어쩌고저쩌고 단어 잔뜩 , ~~ 할 것이다

과거가 왔으니 동사도 맞춰줘야 하지만 사이 단어가 많다면, 초기 레이어로 역전파 하기 힘들 것이다

RNN은 주변 단어에 영향을 많이 받기에 멀리 있으면 학습이 어렵다

 

마찬가지로 기울기 폭발 문제가 있지만, 이건 발견하기 쉽다고 한다 (NaN 같은 경우)

Gradient Clipping은 해결책들 중 하나다

기울기 벡터를 보고, 임계값보다 크면 너무 크지 않게 만들어 주는 것이다

Gated Recurrent Unit (GRU)

기본 RNN에서 장거리 정보를 받아들여 기울기 소실 문제를 줄이는 방법 중 하나를 배워보자

a 대신 memory cell이란 의미로 c를 사용하자 (GRU에선 사실 \(c^{<t>}==a^{<t>}\)이다)

우리는 매 스텝마다 아래의 틸다 식을 계산할 것이다

\(\tilde {c}^{<t>}=tanh(W_c [c^{<t-1>}, x^{<t>}]+b_c)\)

틸다 식은 메모리가 될 후보? 정도로 생각하자

 

GRU의 특징은 게이트로 아래 식으로 계산된다

\(\Gamma_u=\sigma(W_u [c^{<t-1>}, x^{<t>}]+b_u)\)

아래 첨자 u는 업데이트를 의미하며, 0~1 사이에 값을 가진다 (시그모이드 때문에!)

철창문에 감마가 있고 Gㅔ이트 라 감마라는 TMI...

시그모이드에서 값이 크거나 작으면 0 or 1에 근접하기에 일단 0이나 1로 생각해보자

 

자 우리는 문장에서 단수, 복수를 알아야 한다고 생각해보자

The cat, Blah blah ~~ , was full.

\(c^{<t>}\)에 단수면 1, 복수면 0을 저장한다고 생각하자

게이트가 하는 일은 언제 이 c를 업데이트할지이다

이 경우 cat에서 1의 값을 가지고 쭉 유지하다가 was에서 값들이 더 이상 필요 없게 된다

수식으로 보면 아래와 같다

\(c^{<t>}=\Gamma_u * \tilde{c}^{<t>} + (1-\Gamma_u)*c^{<t-1>}\)

아하 이래서 틸다가 후보고, 게이트구나

이런 느낌

감마가 0에 가까워짐에 따라 c는 거의 보존된다

그렇기에 먼 거리의 시퀀스 정보가 오래 저장될 수 있다

즉 기울기 소실 문제 해결이 가능하다

 

근데 사실 이 GRU는 단순화된 유닛이고, 사실 아래와 같이 식이 조금 다르다

\(\tilde{c}^{<t>}=tanh(W_c[\Gamma_r * c^{<t-1>},x^{<t>}]+b_c)\)
\(\Gamma_r=\sigma(W_r[c^{<t-1>},x^{<t>}]+b_r)\)

Long Short Term Memory (LSTM)

GRU 말고 다른 해결책으론 LSTM이 있다

LSTM은 좀 더 일반적인 느낌?

\(c^{<t>}!=a^{<t>}\)이며, 식은 아래와 같이 변한다

\(\tilde{c}^{<t>}=tanh(W_c[a^{<t-1>},x^{<t>}]+b_c)\)
\(\Gamma_u=\sigma(W_u[a^{<t-1>},x^{<t>}]+b_u)\)
\(\Gamma_u=\sigma(W_f[a^{<t-1>},x^{<t>}]+b_f)\)
\(\Gamma_u=\sigma(W_o[a^{<t-1>},x^{<t>}]+b_o)\)

\(c^{<t>}=\Gamma_u * \tilde{c}^{<t>} + \Gamma_f*c^{<t-1>}\)
\(a^{<t>}=\Gamma_o * tanh(c^{<t>})\)

감마 u 게이트와 함께 감마 f(forget) 게이트가 추가되었다

또한 a 값을 구하는 과정에서 감마 o(out put) 게이트가 생겼다

그림으로보면 이렇게 생겼다

감마에 \(c^{<t-1>}\)을 넣는 peephole connection을 추가하여, 이전 메모리를 추가로 참조할 수 있게 구현하기도 한다

 

사실 LSTM이 먼저 개발되고, 후에 GRU가 나오게 되었다

단순하기에, 여러 팀에서 GRU도 사용하고 있다고 한다

Bidirectional RNN

대부분의 RNN 아이디어를 봤지만, 더 강력한 모델을 만들 수 있는 아이디어 두 가지가 남았다

먼저 시퀀스의 전과 후 정보를 모두 사용하는 양방향 RNN을 먼저 배워보자

지금까지 배운 그냥 RNN

한쪽 방향만 본다면 아래 문장에서 판단은 좀 힘들어 보인다

He said, "Teddy bears are on sale!"
He said, "Teddy Roosevelt was a great President!"

Teddy가 등장하기까지 문장이 동일해, 사람 이름인지 아닌지, 판단이 쉽지 않다

 

양방향 RNN은 말 그래도 bidirectional, 시퀀스 전후의 정보도 사용하여 이 문제를 해결한다

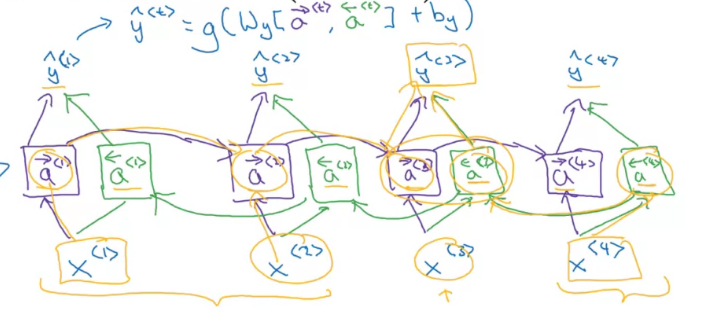
보라색 연산-> 초록색 연산-> 하늘색 연산

느낌으로 값을 예측하게 된다

보통 양방향 RNN에 LSTM을 사용한다고 한다

Deep RNNs

Standard NN에서 히든 레이어를 쌓던 느낌과 비슷하다

표기법은 이전까지 보던 것과 동일하다

3개의 히든 레이어가 있는 deep RNN이다

각 레이어에 \(W, b\) 파라미터는 공유된다

예시로 계산을 하나 보자면 아래와 같다

\(a^{[2]<3>}=g(W_a^{[2]}[a^{[2]<2>},a^{[1]<3>}]+b_a^{[2]})\)

RNN은 시퀀스가 길기에 3개만 해도 되게 깊은 경우라고 한다